搜索与图论

DFS

回溯，剪枝

import java.util.*;

public class Main{
    static int N = 10, n;
    static int[] path = new int[N];
    static boolean[] st = new boolean[N];
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        dfs(0);
    }
    
    public static void dfs(int u){
        if(u == n){
            for(int i = 0; i < n; i++){
                System.out.print(path[i] + " ");
            }
            System.out.println();
            return;
        }
        
        for(int i = 1; i <= n; i++){
            if(!st[i]){
                path[u] = i;
                st[i] = true;
                dfs(u + 1);
                st[i] = false;
            }
        }
    }
}

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

代码：

import java.util.*;

public class Main{
    static int N = 10, n;
    static char[][] chessboard = new char[N][N];
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        for(char[] ch : chessboard){
            Arrays.fill(ch, '.');
        }
        n = in.nextInt();
        dfs(0);
    }
    
    public static void dfs(int row){
         if(row == n){
            for(int i = 0; i < n; i++){
               for(int j = 0; j < n; j++){
                   System.out.print(chessboard[i][j]);
               }
               System.out.println();
            }
            System.out.println();
            return;
        }

        for(int col = 0; col < n; col++){
            if(isValid(row, col)){
                chessboard[row][col] = 'Q';
                dfs(row + 1);
                chessboard[row][col]  = '.';
            }
        }
    }
    
    
    public static boolean isValid(int row, int col){
        for(int i = 0; i < row; i++){
            if(chessboard[i][col] == 'Q'){
                return false;
            }
        }

        for(int i = row, j = col; i >= 0 && j >= 0; i--, j--){
            if(chessboard[i][j] == 'Q'){
                return false;
            }
        }

        for(int i = row, j = col; i  >= 0 && j < n; i--, j++){
            if(chessboard[i][j] == 'Q'){
                return false;
            }
        }

        return true;
    } 
}

BFS

求解最短路问题（边权为1）

DP是特殊的最短路问题（无环）

输入样例：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例
8

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[][] matrix = new int[n][m];
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                matrix[i][j] = scanner.nextInt();
            }
        }
        
        int res = bfs(matrix, n, m);
        System.out.print(res);
    }
    
    public static int bfs(int[][] matrix, int n, int m){
        Queue<Node> queue = new LinkedList<>();
        //将起点添加进队列
        queue.offer(new Node(0, 0));
        //表示从左上角开始到达当前位置走了多远距离
        int[][] dis = new int[n][m]; 
        //利用向量的方法进行上下左右前进
        int[] dx = {-1, 0, 1, 0};
        int[] dy = {0, 1, 0, -1};
        while(!queue.isEmpty()) {
             //每次都处理队列的头结点
            Node node = queue.poll();
             //当扫描到了右下角的位置时说明搜索完毕，退出循环
            if(node.x == n - 1 && node.y == m - 1) {
                break;
            }
            
            for(int i = 0; i < 4; i++) {
                int newx = node.x + dx[i];
                int newy = node.y + dy[i];
                
                 //当新位置在合法范围内并且新位置的元素为0且没有被访问过的请情况下才可以继续查找
                if(newx >= 0 && newy >= 0 && newx < n && newy < m && dis[newx][newy] == 0 && matrix[newx][newy] == 0) {
                    //将新节点添加进队列
                    queue.offer(new Node(newx, newy));
                    //记录距离
                    dis[newx][newy] = dis[node.x][node.y] + 1;
                }
            }
        }
        
        return dis[n - 1][m - 1];
    }
    
}

class Node{
    int x;
    int y;
    
    public Node(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

输入样例
2 3 4 1 5 x 7 6 8
输出样例
19

import java.io.*;
import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        String start = "";
        for(int i = 0; i < 9; i++){
            start = start + scan.next();
        }
        String end = "12345678x";
        int res = bfs(start, end); 
        System.out.print(res);
    }
    
    public static int bfs(String start, String end){
        //队列，用来存储状态
        Queue<String> que = new LinkedList<>();
        //从start走到当前状态的步数（距离）
        Map<String,Integer> map = new HashMap<>();
        //将起点添加进队列
        que.offer(start);
        map.put(start,0);
        
        int[] dx = {-1, 0, 1, 0};
        int[] dy = {0, -1, 0, 1};
        
        
        while(!que.isEmpty()){
            String head = que.poll();
            //找到k在String中的下标
            int k  = head.indexOf('x');
            //然后进行一维数组转化成二维的下标操作
            int x = k / 3 ; int y = k % 3;
            
            int distance = map.get(head);
            
            if(head.equals(end)){
                return distance;
            }
            
            //状态转移
            for(int i = 0; i < 4; i++){
                int a = x + dx[i];
                int b = y + dy[i];
                
                if(a >=0 && a < 3 && b >= 0 && b < 3){
                    char[] arr = head.toCharArray(); 
                    swap(arr, k, a * 3 + b);
                    String s = new String(arr);
                    if(!map.containsKey(s)){
                        map.put(s, distance + 1);
                        que.offer(s);
                    }
                }
            }
        }
        return -1;
    }
    
    public static void swap(char[] arr,int x,int y){
        char temp = arr[x];
        arr[x] = arr[y];
        arr[y] = temp;
    }   
}

树与图的存储

树是无环连通图

无向图可以转化为有向图

邻接矩阵

邻接表： 拉链法

树与图的深度优先遍历

数组建立邻接表

//邻接表
//idx 存储当前要分配的下标
static int idx;
//head数组，存储head指向的节点下标
static int[] h = new int[N];
//e[i] 存储节点i的值，即编号
static int[] e = new int[M];
//ne[i] 表示节点i的next指针,存储下标
static int[] ne= new int[M];

//头插法
static void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

树与图的ddfs模板

// 需要标记数组st[N],  遍历节点的每个相邻的边
void dfs(int u) {
    st[u] = true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            dfs(j);
        }
    }
}

题目

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

本题的本质是树的dfs， 每次dfs可以确定以u为重心的最大连通块的节点数，并且更新一下ans。

也就是说，dfs并不直接返回答案，而是在每次更新中迭代一次答案。

这样的套路会经常用到，在 树的dfs 题目中

import java.io.*;
import java.util.*;

public class Main{
    //邻接表存储方式
    static int N = 100010, M = N * 2, n;
    //idx 存储当前要分配的下标
    static int idx;
    //头节点数组，存储head指向的节点下标
    static int[] h = new int[N];
    //e[i] 表示节点i的值
    static int[] e = new int[M];
    //ne[i] 表示节点i的next指针,存储下标
    static int[] ne= new int[M];
    //标记数组st
    static boolean[] st = new boolean[N];
    static int ans = N;
    
    public static void add(int a, int b){
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    //返回以u为根的子树中节点的个数，包括u节点
    public static int dfs(int u){
        st[u] = true;
        int res = 0;
        int sum = 1;
        
        for(int i = h[u]; i != -1 ; i = ne[i]){
            int j = e[i];
            if(st[j] == false){
                int s = dfs(j);
                res = Math.max(res, s);
                sum += s;
            }
        }
        
        res = Math.max(res, n - sum);
        ans = Math.min(res, ans);
        
        return sum;
    }
    
    public static void main(String[] args){
        Scanner  scan = new Scanner(System.in);
        n = scan.nextInt();
        for(int i = 1 ; i < N ; i++ ){
            h[i] = -1;
        }
        for(int i = 0; i < n - 1; i++){
            int a = scan.nextInt();
            int b = scan.nextInt();
            add(a, b);
            add(b, a);
        }
        
        dfs(1);
        System.out.println(ans);
        
    }
    
}

树与图的宽度优先遍历

层次遍历：每次pop出队时，将与它距离为1的节点全部加到队列中

树与图的bfs模板

queue <- 起点
while queue 不空
{
    t <- 队头
    拓展t的所有邻点s{
         if(s未被遍历过){
             queue <- s;
            d[s] = d[t] + 1;
         }
    }
}

题目

输入样例：

4 5
1 2
2 3
3 4
1 3
1 4

输出样例：

1

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;


public class Main{
    static int N = 100010, n, m, idx;
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] h = new int[N];
    //结点1到结点i的最短距离
    static int[] d = new int[N];
    
    
    public static void add(int a, int b){
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    public static int bfs(){
        Queue<Integer> q = new LinkedList<>();
        q.offer(1);
        d[1] = 0;
        while(!q.isEmpty()) {
            int t = q.poll();
            for(int i = h[t]; i != - 1; i = ne[i]) {
                int s = e[i];
                if(d[s] == -1) {
                    q.offer(s);
                    d[s] = d[t] + 1; 
                }
            }
        }
        return d[n];
    }
    
    
    
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        for(int i = 0; i < N; i++) {
            h[i] = -1;
            d[i] = -1;
        }
        for(int i = 0; i < m; i++) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            add(a,b);
        }
        
        int res = bfs();
        System.out.print(res);
    }

}

拓扑排序

只适用于 AOV网 （有向无环图）

算法流程：

用队列来执行 ，初始化讲所有入度为0的顶点入队。

主要由以下两步循环执行，直到不存在入度为 0 的顶点为止

1. 选择一个入度为 0 的顶点，并将它输出；

2. 删除图中从顶点连出的所有边。

循环结束，

若输出的顶点数小于图中的顶点数，则表示该图存在回路，即无法拓扑排序，

否则，输出的就是拓扑序列 （不唯一）

queue <- 所有入度为0的点
while queue 不空
{
    t <- 队头
    枚举t的所有出边 t -> j{
        删除t -> j, d[j]--;
         if(d[j] == 0){
             queue <- j;
         }
    }
}

题目

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

import java.util.Scanner;


public class Main {
    static int N = 100010, n, m, idx;
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] h = new int[N];
    //数组模拟栈
    static int[] q = new int[N];
    //结点i的入度
    static int[] d = new int[N];
    
    public static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    public static boolean topSort() {
        int hh = 0, tt = -1;
        for(int i = 1; i <= n; i++) {
            if(d[i] == 0) {
                q[++tt] = i;
            }
        }
        while(hh <= tt) {
            int t = q[hh++];
            for(int i = h[t]; i != -1; i = ne[i]) {
                int s = e[i];
                d[s]--;
                if(d[s] == 0) {
                    q[++tt] = s;
                }
            }
        }
        return tt == n -1; 
    }
    
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        for(int i = 0 ; i < N ; i ++ ){
            h[i] = -1; 
         }
        for(int i = 0; i< m; i++) {
            int a = in.nextInt();
            int b = in.nextInt();
            add(a, b);
            d[b]++;
        }
        
        if(topSort() == true){
          for(int i = 0 ; i < n; i ++ ){ 
                System.out.print(q[i] + " ");
            }
        }else {
            System.out.print(-1);
        }
    }

}

最短路

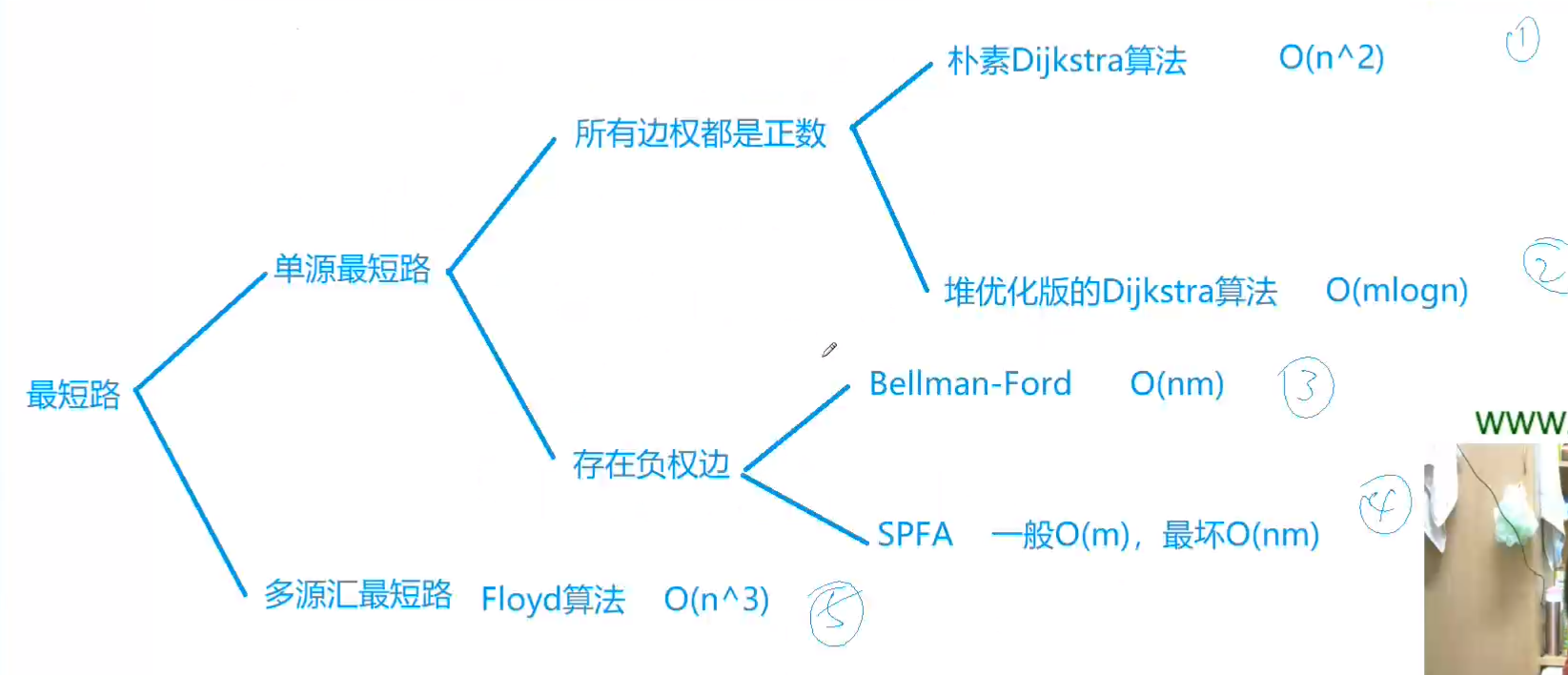
稠密图用邻接矩阵存储

稀疏图用邻接表存储

Dijkstra

Dijkstra 的整体思路：即进行n（n为结点的个数）次迭代去确定每个点到起点的最小值 最后输出的终点的即为我们要找的最短路的距离

朴素版本

适用于稠密图

集合S为已经确定最短路径的点集。

1. 初始化距离
   一号结点的距离为零，其他结点的距离设为无穷大（看具体的题）。
2. 循环n次，每一次将集合S之外距离最短的点 t 加入到S中去（这里的距离最短指的是距离1号点最近。
   点 t 的路径一定最短，基于贪心，严格证明待看）。然后用点t更新 t 邻接点的距离

输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

import java.util.*;
import java.io.*;

public class Main {
    /**
     * Java快速读写模板
     */
    public static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    
    public static int nextInt() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }
    
    public static double nextDouble() throws IOException {
        in.nextToken();
        return in.nval;
    }
    
    public static String nextString() throws IOException {
        in.nextToken();
        return in.sval;
    }

    
    static int N = 510, n, m;
    //邻接矩阵存储图
    static int[][] g = new int[N][N];
    //记录每一个点距离第一个点的距离
    static int [] dist = new int[N];
    //用于记录该点的最短距离是否已经确定
    static boolean[] st = new boolean[N];
    
    public static int dijkstra() {
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[1] = 0;
        
        ////迭代n次，每次可以确定一个点到起点的最短路
        for(int i = 0; i < n; i++) {
            int t = -1;
            //t就是未确定最短路径的点的集合中距离起点最短的点
            for(int j = 1; j <= n ; j++) {
                if(st[j] == false && (t== -1 || dist[j] < dist[t])) {
                    t = j;
                }
            }
            
            //加入到s集合中
            st[t] = true;
            
             //找到了距离最小的点t，并用最小的点t去更新其他的点到起点的距离
            for(int j = 1 ; j <= n ; j ++ ){
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
            }
        }
   
        if(dist[n] == 0x3f3f3f3f) return -1;
        else return dist[n];
    }
    
    public static void main(String[] args) throws IOException {
        n = nextInt();
        m = nextInt();
        
        for(int i = 1 ; i <= n ; i ++){
            Arrays.fill(g[i], 0x3f3f3f3f);
        }
        for(int i = 0; i < m; i++) {
            int a = nextInt();
            int b = nextInt();
            int z = nextInt();
             //如果有重边，保留权值最小的一条边
            g[a][b] = Math.min(g[a][b], z);
        }
        
        int res = dijkstra();
        out.write(res + "");
        out.flush();
    }
}

堆优化版本

适用于稀疏图

堆优化版的dijkstra是对朴素版dijkstra进行了优化，在朴素版dijkstra中时间复杂度最高的寻找距离最短的点O(n^2)可以使用最小堆优化。

1. 一号点的距离初始化为零，其他点初始化成无穷大。
2. 将一号点放入堆中。
3. 不断循环，直到堆空。每一次循环中执行的操作为：
   弹出堆顶（与朴素版diijkstra找到S外距离最短的点相同，并标记该点的最短路径已经确定）。
   用该点更新临界点的距离，若更新成功就加入到堆中。

import java.io.*;
import java.util.*;

public class Main{
    static int N = 100010;
    static int n, m, idx;

    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] w = new int[N];
    static int[] dist = new int[N];// 存储1号点到每个点的最短距离
    static boolean[] st = new boolean[N];
    static int INF = 0x3f3f3f3f;//设置无穷大
    public static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    // 求1号点到n号点的最短路，如果不存在则返回-1
    public static int dijkstra()
    {
        //维护当前未在st中标记过且离源点最近的点
        Queue<int[]> pq = new PriorityQueue<>((a, b) -> {return a[1] - b[1];});
        Arrays.fill(dist, INF);
        dist[1] = 0;
        queue.add(new int(1,0));
        while(!queue.isEmpty())
        {
            //1、找到当前未在s中出现过且离源点最近的点
            int[] p = queue.poll();
            int t = p[0];
            int distance = p[1];
            if(st[t]) continue;
            //2、将该点进行标记
            st[t] = true;
            //3、用t更新其他点的距离
            for(int i = h[t]; i != -1; i = ne[i])
            {
                int j = e[i];
                if(dist[j] > distance + w[i])
                {
                    dist[j] = distance + w[i];
                    queue.add(new int(dist[j], j));
                }
            }

        }
        if(dist[n] == INF) return -1;
        return dist[n];
    }

    public static void main(String[] args) throws IOException{
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        Arrays.fill(h,-1);
        while(m -- > 0){
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            add(a,b,c);
        }
        int res = dijkstra();
        System.out.println(res);
    }
}

Bellman - ford

Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

通俗的来讲就是：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新

for n次
    for 所有边 a,b,w (松弛操作)
        dist[b] = min(dist[b],back[a] + w)

back[] 数组是上一次迭代后 dist[] 数组的备份，由于是每个点同时向外出发，因此需要对 dist[] 数组进行备份，若不进行备份会因此发生串联效应，影响到下一个点

输入样例：

3 3 1
1 2 1
2 3 1
1 3 3

输出样例：

3

import java.util.Arrays;
import java.util.Scanner;


class Edge{
    int x,y,z;
    public Edge(int x,int y,int z){
        this.x = x;
        this.y = y;
        this.z = z;
    }
}

public class Main {
    static int N = 510, M = 10010, n, m, k;
    static int[] dist = new int[N];
    static int[] back = new int[N];
    static Edge[] edgs = new Edge[M];
    
    static void bellman_ford() {
        Arrays.fill(dist, (int)1e9);
        dist[1] = 0;
        for(int i = 0; i < k; i++) {
            back = Arrays.copyOf(dist, n + 1);
            for(int j = 0; j < m; j++){
               Edge edg = edgs[j]; //每一条边的结构体 
                int a = edg.x;     
                int b = edg.y;
                int c = edg.z;
                dist[b] = Math.min(dist[b], back[a] + c); //用上面的点来更新后面的点
            }
        }
        
        if(dist[n] > (int)1e9 / 2) System.out.println("impossible");
        else System.out.println(dist[n]);        
    }
    
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        k = in.nextInt();
        for (int i = 0; i < m; i++) {
            int x = in.nextInt();
            int y = in.nextInt();
            int z = in.nextInt();
            edgs[i] = new Edge(x, y, z);
        }
        
        bellman_ford();
    }

}

SPFA

spa求最短路

Bellman_ford算法会遍历所有的边，但是有很多的边遍历了其实没有什么意义，我们只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点。

SPFA算法和Dijstra算法

SPFA可以处理负权边，但是不能处理有负权回路的图；而Dijkstra不能处理带有负权边和负权回路的图，因为Dijkstra算法在计算最短路径时，不会因为负边的出现而更新已经计算过(收录过)的顶点的路径长度；

st数组

• Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点，且一旦确定了最小那么就不可逆了(不可标记为true后改变为false)；
• SPFA算法中的st数组仅仅只是表示的当前发生过更新的点，且spfa中的st数组可逆(可以在标记为true之后又标记为false)。
• 顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。

队列

• Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点，目的是快速的取出当前到源点距离最小的点；
• SPFA算法中使用的是队列(也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。

输入样例：

3 3
1 2 5
2 3 -3
1 3 4

输出样例：

2

import java.util.*;
import java.io.*;


public class Main {
    static int N = 100010;
    static int n, m, idx;

    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] w = new int[N];
    static int[] dist = new int[N];// 存储1号点到每个点的最短距离
    static boolean[] st = new boolean[N];//判断当前的点是否已经加入到队列当中了；
    static int INF = 0x3f3f3f3f;//设置无穷大
    public static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    // 求1号点到n号点的最短路，如果不存在则返回-1
    public static void spfa()
    {
       
        Arrays.fill(dist, INF);
        dist[1] = 0;
        
        //声明一个队列保存更新过的节点
        Queue<Integer> q = new LinkedList<>();
        q.offer(1);
        st[1] = true;
        
        while(!q.isEmpty()) {
            int t = q.poll();
            st[t] = false;
            for(int i = h[t]; i != -1; i = ne[i]) {
                int j = e[i];
                 //如果当前节点可以被更新，就做更新操作，并将该节点加入到队列中
                if(dist[j] > dist[t] + w[i]) {
                    dist[j] = dist[t] + w[i];
                    if(st[j] == false) {
                        q.offer(j);
                        st[j] = true;
                    }
                }
            }
        }
        
        if(dist[n] == INF) System.out.println("impossible");
        else System.out.println(dist[n]);
    }

    public static void main(String[] args) throws IOException{
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        Arrays.fill(h,-1);
        while(m -- > 0){
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            add(a,b,c);
        }
        spfa();
    }
}

spa求负环

统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环

输入样例：

3 3
1 2 -1
2 3 4
3 1 -4

输出样例：

Yes

import java.util.*;
import java.io.*;


public class Main {
    static int N = 100010;
    static int n, m, idx;

    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] w = new int[N];
    static int[] dist = new int[N];// 存储1号点到每个点的最短距离
    static boolean[] st = new boolean[N];//判断当前的点是否已经加入到队列当中了
    static int[] cnt = new int[N];//1到i的最短路径边数
    static int INF = 0x3f3f3f3f;//设置无穷大
    public static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    // 求1号点到n号点的最短路，如果不存在则返回-1
    public static boolean spfa()
    {
       
        //Arrays.fill(dist, INF);
        dist[1] = 0;
        
        //声明一个队列保存更新过的节点
        Queue<Integer> q = new LinkedList<>();
        //可能起点到不了负环，所以将所有的点都加入到队列中去
        for(int i = 1; i <= n; i++){
            q.offer(i);
            st[i] = true;
        }
        
        while(!q.isEmpty()) {
            int t = q.poll();
            st[t] = false;
            for(int i = h[t]; i != -1; i = ne[i]) {
                int j = e[i];
                 //如果当前节点可以被更新，就做更新操作，并将该节点加入到队列中
                if(dist[j] > dist[t] + w[i]) {
                    dist[j] = dist[t] + w[i];
                    cnt[j] = cnt[t] + 1;
                    
                    if(cnt[j] >= n) return true;
                    if(st[j] == false) {
                        q.offer(j);
                        st[j] = true;
                    }
                }
            }
        }
        
        return false;
    }

    public static void main(String[] args) throws IOException{
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        Arrays.fill(h,-1);
        while(m -- > 0){
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            add(a,b,c);
        }
        if(spfa() == true) System.out.println("Yes");
        else  System.out.println("No");
    }
}

Floyd

多源汇最短路问题-具有多个源点

输入样例：

3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3

输出样例：

impossible
1

import java.util.Scanner;

public class Main {
    static int N = 210, INF = (int)1e9, n, m, k;
    static int[][] d = new int[N][N];
    /**
    f[k][i][j]代表（k的取值范围是从1到n），在考虑了从1到k的节点作为中间经过的节点时，从i到j的最短路径的长度。
    f[k][i][j]可以从两种情况转移而来：
    【1】从f[k−1][i][j]转移而来，表示i到j的最短路径不经过k这个节点
    【2】从f[k−1][i][k]+f[k−1][k][j]转移而来，表示i到j的最短路径经过k这个节点
    */
    static void floyd() {
        for(int k = 1; k <= n; k++) {
            for(int i = 1; i <= n; i++) {
                for(int j = 1; j <= n; j++) {
                    d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
                }
            }
        }
    }
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        k = in.nextInt();
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if(i == j) d[i][j] = 0;
                else d[i][j] = INF;
            }
            
        }
        
        while(m-- > 0) {
            int a = in.nextInt();
            int b = in.nextInt();
            int c = in.nextInt();
            d[a][b] = Math.min(d[a][b], c);
        }
        
        floyd();
        
        while(k-- > 0) {
            int x = in.nextInt();
            int y = in.nextInt();
            if (d[x][y] > INF / 2) System.out.println("impossible");
            else System.out.println(d[x][y]);
        }
    }
}

最小生成树

最小生成树：给定一个无向图，在图中选择若干条边把图的所有节点连起来，要求边长之和最小

应用场景：地图上，有n个城市，知道坐标，要在城市之间铺设公路，让城市相互连通，铺设最小距离是多少

Prim

prim 算法采用的是一种贪心的策略：

每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

Prim算法与Dijkstra算法的区别：

Dijkstra算法是更新不在集合中的点 离起点的距离

dist[j]=min(dist[j], dist[t]+g[t][j])

Prim是更新不在集合中的点 离集合S的距离

dist[j] = min(dist[j], g[t][j])

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

6

import java.io.*;
import java.util.*;

public class Main{
    static int N = 510, INF = 0X3F3F3F3F, n, m;
    static int[][] g = new int[N][N];
    static int[] dist = new int[N];//点到连通部分的距离
    static boolean[] st = new boolean[N];//表示节点是否已经连通
    
    static int prim(){
        Arrays.fill(dist, INF);
        int res = 0;
        //迭代n次找出n个点
        for(int i = 0; i < n; i++){
            int t = -1;//t表示还没有找到数
            //找到离连通部分最近的点
            for(int j = 1; j <= n; j++){
                if(!st[j] && (t == -1 || dist[j] < dist[t])){
                    t = j;
                }
            }
            
            //第一次任选一个点为起点，不更新res
            if(i > 0){
                //如果这个点的距离是正无穷，说明没有连通，结束返回INF
                if(dist[t] == INF) return INF;
                res += dist[t];   
            }
            st[t] = true;
            
             //用t去更新其他集合外面的点
            for (int j = 1; j <= n; j ++ ) dist[j] = Math.min(dist[j], g[t][j]);
        }
        return res;
    }
    
    
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        for(int i = 1 ; i <= n ; i ++ ){
            Arrays.fill(g[i],INF);
        }
        while(m-- > 0){
            int u = in.nextInt();
            int v = in.nextInt();
            int w = in.nextInt();
            g[u][v] = g[v][u] = Math.min(g[u][v], w);
        }
        
        int res = prim();
        if(res == INF) System.out.println("impossible");
        else System.out.println(res);  
    }
}

Kruskal

并查集判断点a，b是否连通(属于同一集合)

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

6

import java.io.*;
import java.util.*;

public class Main{
    static int N = 100010, n, m;
    static int[] p = new int[N];
    
    //并查集模板，所有的集合在过程中全部指向根节点
    public static int find(int x){ 
        if(p[x] != x) p[x] = find(p[x]);
        return  p[x];
    }
    
    static void  kruskal(Edge[] g){
        Arrays.sort(g, new Comparator<Edge>(){

           @Override
           public int compare(Edge e1, Edge e2){
               return e1.c - e2.c;
           }
        });
        
        int res = 0;
        int cnt = 0;
        //枚举所有的边
        for(int i = 0; i < m; i++){
            int a = g[i].a;
            int b = g[i].b;
            int c = g[i].c;
            //判断一下a和b是不是在同一个集合中，不在集合中执行以下操作
            a = find(a); b = find(b);
            if(a != b){
                p[a] = b; //将两个集合合并
                res += c;//res增加权重
                cnt ++;//边数加1
            }
        }
        if(cnt < n - 1) System.out.println("impossible");
        else System.out.println(res);
    }
    
    
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        Edge[] g = new Edge[m];//存储边
        for(int i = 1 ; i<= n ; i ++ ) p[i] = i;
        for(int i = 0 ; i < m ; i ++ ){
            int u = in.nextInt();
            int v = in.nextInt();
            int w = in.nextInt();
            g[i] = new Edge(u, v, w);
        }
        kruskal(g);
    }
}

class Edge{
    int a,b,c;
    public Edge(int a, int b, int c){
        this.a = a;
        this.b = b;
        this.c = c;
    }
}

二分图